滤池冲洗最佳膨胀率的探讨
一般生产滤池采用非均匀砂层。计算其最佳膨胀率应使截泥最大的表层砂获得最大冲洗功率,即孔隙比达到0.74,从而取各层的平均值。可求得某一砂层的最佳膨胀率为52%,而粒径较大的砂层则可小些。
建议设计滤池冲洗水强度时,以表层砂孔隙比达到0.74为准。
快滤池用于公共给水,约有一百多年的历史,但是设计和运行多半凭经验,而其中滤池冲洗强度及最佳膨胀率为国内外研究滤池的重要课题。
本文从颗粒材料水力学的观点出发,提出滤池冲洗时,冲洗水所提供的冲洗功,从而求得滤层最佳孔隙比及最佳膨胀比(率),以与国内外同行探讨。
一、滤层冲洗时水力学流态
冲洗水由下而上流经滤层时,实质上是一种反向过滤,开始为砂层逐步膨胀,污浊水开始流出的挤压出流阶段;当冲洗水达到一定流速后,滤层膨胀,砂粒悬浮于水中,处于一种不停地运动的动平衡状态,即达到固定膨胀阶段,此时砂粒表面被水流冲刷,砂粒之间互相碰撞,小颗粒在上面,大颗粒在下面。冲洗水流速愈大,滤层膨胀率愈大。
上升流速——对于均匀颗粒砂层.MHHH曾得出流速v与滤层孔隙比m的关系式。
Re=Pwvd/6μ(1-m)a(1)
n=Pm3d/LPwv26(1-m)a (2)
通过实验求得:
n=A/Re0.7 (3)
式中:
a——砂粒形状系数(砂为1,煤为1.31)
Pw——水的密度(g/cm3)
d——粒径(cm)
μ——水的粘滞系数(g/cm·s)
m——砂层孔隙比
P/L——单位厚度砂层水压降(g/cm2·s2)
A——常数(砂层3.73,煤层5.90)
a——滤层阻力系数
Re——雷诺数
L——滤层厚度(cm)
对于悬浮砂层
P/L=(Ps-Pw)g(1-m)(4)
g——重力加速度(cm/s2)
Ps——砂的密度(g/cm3)
将(1),(2),(4)式代入(3)式,得冲洗水上升流速表达式:
v=(g/A61.7)0.77
(Ps-Pw)0.77d1.31m2.31/a1.31Pw0.23μ0.54(1-m)0.54(cm/s) (5)
砂粒对水的阻力[1]——冲洗水以流速v/m通过悬浮均匀砂层,受到来自砂粒的阻力。单位砂层厚度水压降P/L即等于单位体积悬浮层的阻力。
单位体积悬浮砂层中砂粒数
N=6(1-m)/πd3 (6)
每一砂粒的阻力为
Fφ=P/LN=Pπd3/L·6(1-m) (g·cm/s2) (7)
从(2)式可知
P/L=n·Pwv2·6(1-m)a/m3d (g/s2·cm/s2)(8)
将(8)式代入(7)式得
Fφ=n·Pwv2 d2πa /m3 (g·cm/s2)(9)
将(3)式代入(9)式,悬浮砂层中每一粒砂砂对水的阻力
Fφ=3.73×60.7·μ0.7(1-m)0.7Pw0.3 1.3πd1.3a1.7/m3(10)
水对砂层所作冲洗功——冲洗水克服阻力Fφ,并以相对流速v/m流过砂粒,则水对单位体积膨胀砂层作所作之功率为:
Ws=Fφ·v/m·N(g/s3·cm) (11)
=6920·(Ps-Pw)1.771d1.313·m1.313(1-m)0.458/a1.313Pw0.229μ0.542
(12)
当水温为20℃,μ=0.010,Ps=2.65,Pw=1.00时
Ws=203000d1.313m1.313(1-m)0.458
这是唯一的功率,赋予砂粒的动能,使砂粒悬浮并保持一定的空隙比,使砂粒不停地(平移和旋转)运动,砂粒被冲洗清洁,此外无其他能量来源。
从这一冲洗功率可以算出水流的时均流速梯度G
单位时间内,单位体积悬浮砂层砂粒之间的碰撞次数为
|N|=4/3·N2Gd3 (14)
[注]此式仅适用于层流流态。滤池冲洗时水的流态属过渡区,故此式不适用。然而作为定性地说明问题也还是可以的,与本文的论点及数学推导无关。
可见最大功率赋予冲洗中的砂层以最大的冲洗流速梯度及砂粒之间的碰撞次数,无疑将有最好的冲洗效果。
最佳孔隙比——对应于一个最佳砂层孔隙比,将有一个最大冲洗功率,并由下列条件决定。
dWs/dm=0 (15)
-0.458m+1.313(1-m)=0 (15’)
因之最佳孔隙比
mop=0.741(16)
与之相应的最大冲洗功率
Ws=73700d1.313 (17)
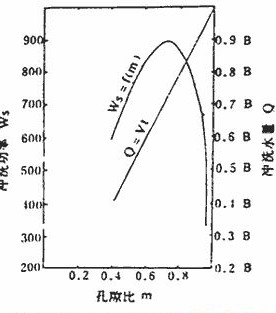
当d=0.0343cm时,冲洗功率W,随孔隙比变化的曲线见下图。
 |
二、最佳膨胀比(率)
若砂层的原有孔隙比m0=0.40,则均匀颗粒滤层冲洗时的最佳膨胀率应为:
Eop=e×100=m-m0/1-m×100
=0.74-0.40/1-0.74=130% (18)
一般生产滤池都采用非均匀颗粒滤层,最佳膨胀率应按砂层组成,分层计算而加和之。
Eop=∫p=100
∫p=0 m-m0/1-mdP%(19)
或
Eop=Σm1-m0/1-m1·△P1(19’)
式:△P1——砂层组成百分率
m1——砂层孔隙比
按照滤池表面10~15cm的砂层截泥最大这一普遍现象,冲洗时,表面砂层的砂粒或者说最小砂粒,应使其膨胀后孔隙比达到0.74,即达到最佳数值。非均匀砂层膨胀后,最小粒径砂层孔隙比达到0.74时,整个砂层的膨胀率为最佳膨胀率,使最小粒径dm的砂层孔隙比mm达到0.74的冲洗水流速,可按(5)式计算,而在同一冲洗流速下不同粒径砂层孔隙比亦可因之而求得。从(5)式
dm1.31·mm2.31/(1-m)0.54=d1.31·m2.31/(1-m)0.54(20)
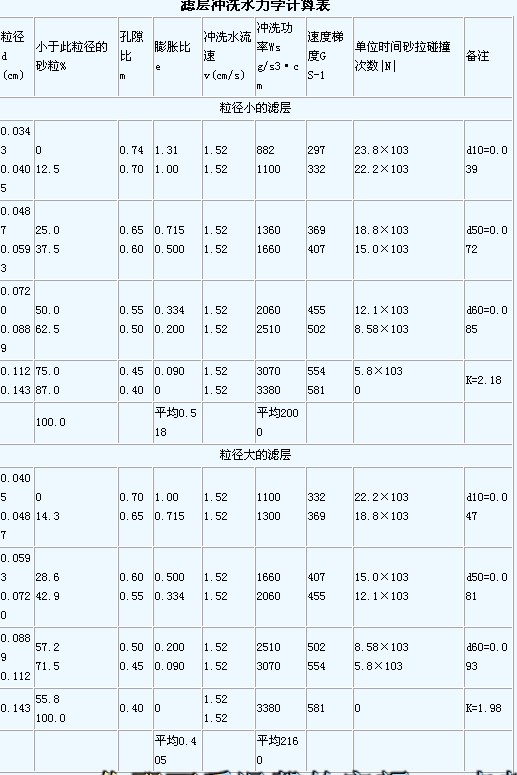
在同一冲洗流速v=1.52cm/s(15.2L/S·m2)下,两不均匀颗粒滤层膨胀后的孔隙比m,膨胀比e,冲洗功率W,时均流速梯度G,砂粒碰撞数∣N∣见下表。
从下表可见,粒径小的滤层,最佳膨胀率为51.8%。粒径大的滤层,最佳膨胀率为40.5%。砂层组成决定最佳膨胀率大于、等于或小于50%。使最小粒径砂层孔隙比达到0.74有决定性意义,建议设计滤池冲池强度以此为准。
三、讨论和推论
1.冲洗时间
截留于一个单位体积滤层的泥量为б,对于膨胀滤层单位体积截泥比бexp为
бexp=б/1+e=1-m/1-m0·б
式中:
б——截泥比,截泥体积和砂层体积之比。
e——砂层膨胀比。
显然,冲洗功应与截泥量成正比:
W=Wst=Fφv/m·Nt=k·(1-m)/(1-m0) б(21)
式中:
t——冲洗时间(s)
k——比例常数,随水,水中悬浮物和砂粒三者的物理化学特性而定。它的大小表示水中悬浮物与砂粒结合的牢固程度,结合力的大小,并受到所用混凝剂、助凝剂的性质及剂量的影响。
T=б/(1-m0)·k(1-m)/Fφ·v/m·N(22)
将(12)式代入(22)式并乘以(5)式,将m以外各参数合并为B,可得
Q=vt=Bm (23)
Q为单位面积砂层冲洗用水量,与砂层膨胀后的孔隙比成正比(见前图)。表层孔隙比愈大,冲洗用水愈多,孔隙比超过0.74,冲洗水量增加,冲洗功率反减少。从经济角度看0.74是上限,下限视(22)式中k值的大小来决定。
应在选定冲洗强度下,使表层砂冲洗清洁所需时间为决定冲洗时间。如冲洗前已知表层砂的截泥比б,通过试验,按(22)式可求得k值。
2.滤池池型
滤池截留水中悬浮物,从上到下砂层截泥逐渐减少。下部没有能发挥其净水作用,而冲洗砂层时,冲洗水对它所作的冲洗功率却很大,这是普通滤池存在的一个矛盾。双向滤池,双层滤池,反滤滤池在不同程度上解决了这一矛盾。但必须使底部砂层充分悬浮,这是易于忽略的。其原因可能是反向滤池底层和双向滤池下层下易冲洗清洁的缘故。
本文所讨论的理论对无烟煤滤池或双层滤池也是适用的。
 |

使用微信“扫一扫”功能添加“谷腾环保网”









