污水高排放标准稳定达标的分析与评价
近年来污水处理高排放标准的稳定达标逐渐成为行业关注的热点,与稳定达标密切相关的出水水质数据分布规律可以用数理统计的方法进行分析。在确定数据分布的基础上,可靠性理论可用于量化分析污水处理的稳定达标。稳定达标率的不同评价周期对投资运行费用具有重要的影响。
随着中国污水处理行业的纵深发展,污水处理的“高排放标准”与“稳定达标”成为行业发展中的热点问题,特别是“如何评价稳定达标”更是成为实际污水处理设计与运行的焦点问题。显然,“高排放标准”与“稳定达标”两者存在密切的关系,排放标准越严,稳定达标的难度越大,反之亦然。围绕这一问题的实践正在不断影响着国内污水处理厂的工艺设计、运行管理及投资与运行的成本。
01 污水处理厂出水水质数据的分布规律
从活性污泥法诞生至今,现代污水处理工艺的发展已经走过百年历程,目前现代污水处理技术基本上是基于活性污泥法的各种变型工艺(如AAO、SBR、氧化沟、IFAS、MBR等)。活性污泥法的稳定性关系到污水处理工艺的稳定性,传统污水处理厂的设计都是基于稳态的设计,但众所周知实际污水处理厂的运行很少是完全稳态的状态,时刻处于动态变化之中,进水负荷的波动、外界环境的变化(降雨和气温等)、运行控制参数的变化、设备的检修维护等因素是客观存在的因素,这些因素使污水处理厂始终处于动态的变化之中,而这种动态变化的可以用数理统计的方法来进行分析。
显然,出水超标与出水水质数据的分布规律有密切关系,如果知道了出水水质数据的分布函数就可以算出超标的概率,并且可以预测未来一段时间内污水处理厂的出水水质情况。大量的研究结果表明,污水处理厂的出水水质基本服从对数正态分布规律,这一结论在欧美的很多污水处理厂都得到了证实。为了进一步证实该结论对国内污水处理厂的适用性,本研究对国内北方某20万m³/d的氧化沟污水处理厂一年出水的COD、氨氮、总氮与总磷的数据分布规律进行了正态分布、对数正态分布、伽马分布的检验,检验方法采用柯尔莫哥洛夫-斯米尔诺夫检验(即K-S检验),统计分析软件采用Statgraphics 18,图1是出水水质数据的直方图与概率分布函数。
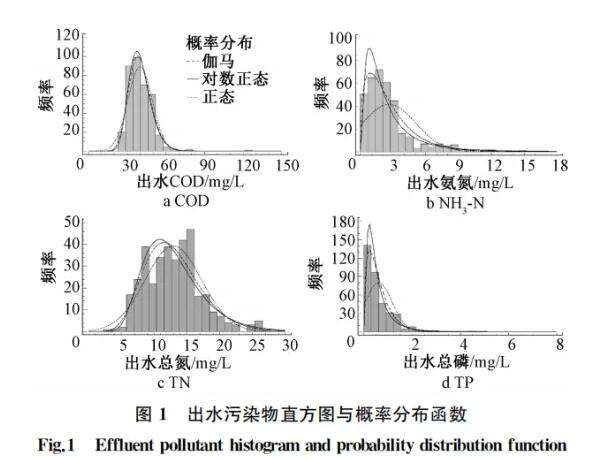
图2是出水水质数据对数的概率图,可以看出图2中基本是直线。上述研究结果表明,该污水处理厂的出水水质数据服从对数正态分布(出水总氮数据同时服从伽马分布),与国外的研究结果类似。

另外从数理统计的角度来看,如果一个变量可以看成是许多很小独立因子的乘积,则这个变量可以看作是对数正态分布。现有的生物动力学模型对COD、氨氮、总氮、总磷的表达含有乘法的规则。因此,出水水质分布从更广的意义上采用对数正态分布表达是合理的。
02 出水水质稳定达标的分析
目前,行业内对“稳定达标”一词并没有明确的定义,如何理解、衡量稳定达标也存在不同的看法。事实上,稳定达标在一定程度上反映了污水处理系统的可靠性,如果可靠性很高则稳定达标相对容易,相反如果系统的可靠性很差则稳定达标也较难。
对于污水处理厂或处理工艺的可靠性,《Wastewater Engineering Treatment and Resource Recovery》给出了明确的定义:即在一定条件下,污水处理厂出水水质的达标时间占考核时间的百分比。比如,某污水处理厂可靠度为99%即是在99%的考核时间内都达标,如果考核的时间是1年,那么将会有3~4 d(3.65 d)的时间超标。因此,“稳定达标”可以用系统的可靠性来衡量评价,即稳定达标率可用可靠度来衡量。由于污水处理厂出水水质波动性的特点,污水处理厂的设计出水水质应该考虑在一定可靠性的基础上低于相应的排放标准,而不能正好是排放标准。
对可靠性的衡量,Niku在1979年提出了可靠性系数的概念,并被推荐为污水处理设计取值的依据。可靠性系数定义为:COR=设计浓度/排放标准,设计的出水平均值进而可以表达为式(1):
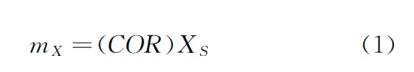
式中 mX——设计运行的出水平均值;
XS——出水标准值;
COR——可靠性系数。
由于上述污水处理厂的出水水质数据服从对数正态分布,因此对数正态分布可用于预测污水处理厂的出水水质性能和可靠性。同时,Niku就如何评估活性污泥法的稳定性进行了深入研究,提出了基于对数正态分布规律的出水水质可靠性系数表达,见式(2):
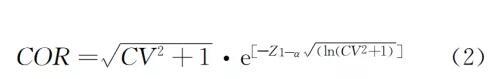
式中 CV——变异系数(Coefficient of Variation),又称“离散系数”,其定义为标准差与平均值之比(σ/μ)。
例如,当CV=0.5、要求稳定达标率为95%时,α=0.05,1-α=0.95,则Z1-α可以从标准正态分布表中查得,Z1-α=1.645。可靠性系数COR可算出COR=0.51。
这就意味着,为了实现出水稳定达标的概率为95%,出水的平均值mX=0.51XS。如果出水氨氮的标准是3 mg/L,则需要设计的出水氨氮值应为0.51×3=10.5(mg/L)才能保证出水稳定达标的概率达到95%(每月约有1.5 d超标)。
这样,通过可靠性系数COR与变异系数CV可以在3个方面有所应用,首先可以对新设计的污水处理厂预期其未来的水质变化,确定合理的设计浓度来满足当前的排放标准。其次,对已有的污水处理厂,可以预测其在同等运行操作工况下的出水超标风险(或出水超标的次数),在某种程度上这也是大数据在智慧水务方面的一个应用;最后,上述方法对于标准的制定者也非常有用,如果知道了污水处理厂或工艺的变异系数CV值,可以制定合理的排放标准。
显然,数据的离散性关系到可靠性系数的高低,出水水质数据的离散性越高,其稳定达标的可靠性就越低;对于离散系数相同的数据,要求稳定达标的可靠度越高,其可靠性系数也越低,如图3所示。

在Niku的研究基础上,Oliveira提出了用于比较污水处理厂和工艺的可靠度计算方法,见式(3):
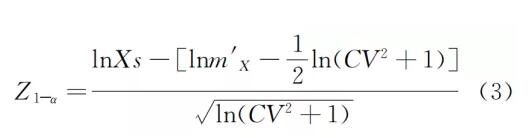
式中 Z1-α——分位数;
m′X——实际出水值。
例如,当出水标准总氮为15 mg/L、CV=0.33、出水总氮实际均值为12 mg/L,则计算得:Z1-α=0.855。
查标准正态分布表,对于Z1-α=0.855,相应的1-α=0.8。这表明该污水处理厂在保持同样的运行条件下,出水TN达到15 mg/L的可靠度是80%,即在考核时间的80%内可以达标。
03 稳定达标的评价
污水处理厂的稳定达标与进水负荷的特性、工艺设计、运行控制等因素有密切关系,采用什么样的方法来评价稳定达标关系到污水处理厂的整体投资与运行费用。
对于污水处理技术的稳定性评价,美国WERF提出了技术性能统计(TPS,Technology Performance Statistic)的概念,技术性能统计是应用数理统计方法来描述技术的性能。技术性能统计分为三个层次,包括理想技术性能、平均技术性能和可靠技术性能,技术性能统计为污水厂的管理者、设计者以及标准的制定者提供了有效的方法来分析工艺达到既定标准的能力。
理想技术性能统计代表可观察的最低浓度,只能维持很短的一段时间。WERF的研究报告认为理想技术性能统计浓度是在一年内持续2周时间的最低浓度(简称,TPS-14),因为在一年52周的时间内将有50周的时间超过上述标准,显然这一标准不能成为评价污水处理厂的标准。理想性能(TPS-14)只是当污水处理厂所受影响因子最小时的统计特性,这种表现只有在受控的实验室里才可重复。之所以采用14 d作为衡量理想技术性能是因为绝大多数生物脱氮除磷工艺的泥龄约8~20 d,14 d的时间对绝大部分污水处理厂是一个完整泥龄的运行时间。
平均技术性能(TPS-50%)主要用来反映可靠性能与平均性能的偏离程度,这里用的并不是一年之中的平均值,而是统计学上的中位值,中位值不受极端变量值的影响。
可靠技术性能是基于技术、考核时间段以及运行者在自身风险承受能力基础上可接受的超标次数而综合确定的百分比,如TPS-90%、TPS-95%、TPS-99%等。图4反映了可靠度与月均值超标数之间的关系,由图可以看出如果在5年之内要求只能有1个月均值超标,则可靠度可达到98%,但是显然会显著增加污水处理厂的投资与运行费用。而如果在5年之内可以有3个月均值超标,可靠度则为95%,但是投资与运行费用会降低很多。

WERF的研究报告表明美国污水处理高排放标准倾向于采用TPS-95%,主要是考虑到美国的很多污水处理厂的排放标准是月均值,也就是如果在连续5年的运行中,超标的月均值可以有3次,这样的结果通常被认为技术是可靠的。
目前,国内的污水处理排放标准一般按照日均值考核,日均值的稳定达标与月均值的稳定达标显然不同,美国环保局推荐用99.7%的可靠度来评估最大日均值,这主要是考虑到当数据近似服从正态分布时,数值分布3个σ之内的概率是99.7%。美国环保局对不同污水处理工艺在不同评估周期的出水数据变化进行一定的统计,部分统计结果如表1所示。
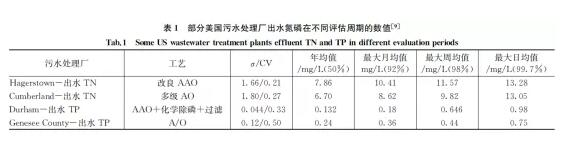
从表1可以看出,最大日均值与年均值、最大月均值之间存在有很大的差异,比如Hagerstown厂的出水TN最大日均值为13.28 mg/L,年均值为7.86 mg/L,最大日均值为年均值的1.7倍,Durham厂的出水TP最大日均值是年均值的7.4倍。WERF的研究报告也显示,美国一些要求高标准脱氮除磷污水处理厂其总氮去除的TPS-14一般是TPS(50%)的50%~60%,TPS(95%)是均值的180%~250%;对于总磷而言,总磷去除的TPS-14值是均值的40%~59%,TPS(95%)是均值的200%~300%,这清楚地表明即使是在美国最好性能的脱氮除磷污水处理厂,出水水质也存在较大的波动性。
采用前文所述的分析方法可以计算出为满足日均值稳定达标的设计浓度,比如某污水处理厂要求出水TN日均值<15 mg/L,在不同的达标率以及CV值情况下,设计的出水TN浓度见表2。
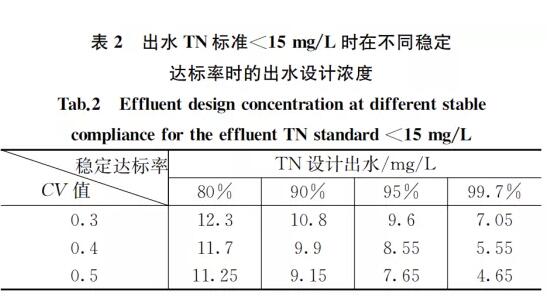
从表2可以看出,如果要求出水TN日均值<15 mg/L的稳定达标率为99.7%,当离散系数CV为0.3~0.5时,出水TN的设计浓度要达到4.65~7.05 mg/L。类似计算,如果要求出水TN日均值<10 mg/L的稳定达标率为99.7%,出水TN的设计浓度要达到3.1~4.7 mg/L,已经接近于生物处理的极限脱氮水平。这无论是对于投资还是运费费用都将是显著的增加。如果要求稳定达标率为80%,为达到小于15 mg/L的TN标准,设计的出水TN浓度为11~12 mg/L(CV 0.3~0.5),这样会显著降低投资与运行费用,但一年中超标的概率将有73天,显然目前从污水处理厂以及监管部门角度来看是难以接受的。
因此,以采用日均值为考核需要在稳定达标率与投资运行费用方面做出平衡选择,这样的选择在很多情况下是非常困难的。现代污水处理的主流技术仍然是基于活性污泥法的各种工艺变型,评估其水质变化的特点至少应在1个泥龄以上的时间,因此采用月均值无论对实现稳定达标还是对投资运行费用的影响相对更为合理,也更易于接受。
04 结语
(1)污水处理厂的出水水质数据可以采用数理统计的方法进行分析,本文采用K-S检验方法,证实了某20万m³/d氧化沟工艺污水处理厂的出水COD、氨氮、总氮、总磷数据服从对数正态分布。
(2)污水处理厂的稳定达标可以采用可靠度分析来进行量化评估,这一方法通过可靠性系数(COR)与离散系数(CV)的相关计算,具体量化了在一定稳定达标率的前提下需要确定的设计浓度,或在同样运行操作条件下目前实际出水水质能够获得的达标率。
(3)污水处理厂出水的最大日均值、最大月均值、年均值之间存在明显的差异,以生物处理为基础的污水处理工艺以月均值评估更为合理。同时,污水处理厂的设计、管理者需要在稳定达标率与投资运行费用之间做出合理的选择。

使用微信“扫一扫”功能添加“谷腾环保网”









